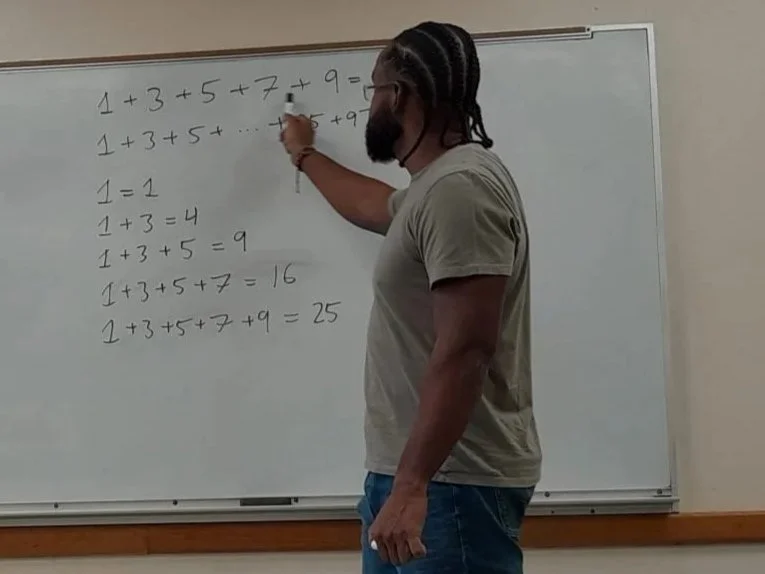Think. Solve. Succeed.
Empowering Bermuda’s Next Generation of Problem Solvers
At Bermuda Mathematics Academy, we make maths easy, enjoyable, and inspiring. Through personalized tutoring, public lectures, and olympiad competitions, we help students and adults alike build confidence, curiosity, and a lifelong appreciation for problem solving.
Meet the Team
Dr. Kevin Minors, PhD
Dr. Minors is a Bermudian mathematician with a passion for solving hard problems, explaining complex ideas simply, and creating those ‘Aha!’ moments. He completed his undergraduate studies in mathematics at the University of Oxford and received his doctorate in mathematics from the University of Bath (his thesis is here). SCARS certificate is here. In his spare time, you will find him working out, dancing salsa, or overwatering his plants.
Student feedback: “one of the better tutors”, “Kevin is the only reason I may pass this module”, “This tutorial will single-handedly get me through this unit - thank you!”
Problem of the Week
Below are some laws of addition and multiplication.
A1 (The Commutative Law for Addition): For any two numbers a and b, a + b = b + a
A2 (The Associative Law for Addition): For any three numbers a, b, and c, a + (b + c) = (a + b) + c
A3 (Additive Identity): For any number a, 0 + a = a
M1 (The Commutative Law for Multiplication): For any two numbers a and b, ab = ba
M2 (The Associative Law for Multiplication): For any three numbers a, b, and c, a(bc) = (ab)c
M3 (Multiplicative Identity): For any number a, 1a = a
D (Distributive Law): For any three numbers a, b, and c, (a + b)c = ac + bc
Using these rules explicitly, prove that -1 x -1 = 1
-
1) Prove there are infinitely many primes.
2) Prove that the square root of 2 is irrational.
3) Below are some laws of addition and multiplication.
A1 (The Commutative Law for Addition): For any two numbers a and b, a + b = b + a
A2 (The Associative Law for Addition): For any three numbers a, b, and c, a + (b + c) = (a + b) + c
A3 (Additive Identity): For any number a, 0 + a = a
M1 (The Commutative Law for Multiplication): For any two numbers a and b, ab = ba
M2 (The Associative Law for Multiplication): For any three numbers a, b, and c, a(bc) = (ab)c
M3 (Multiplicative Identity): For any number a, 1a = a
D (Distributive Law): For any three numbers a, b, and c, (a + b)c = ac + bc
Using these rules explicitly, prove that 0 x 2 = 0, where 2 is defined as 2 = 1 +1
4) Below are some laws of addition and multiplication.
A1 (The Commutative Law for Addition): For any two numbers a and b, a + b = b + a
A2 (The Associative Law for Addition): For any three numbers a, b, and c, a + (b + c) = (a + b) + c
A3 (Additive Identity): For any number a, 0 + a = a
M1 (The Commutative Law for Multiplication): For any two numbers a and b, ab = ba
M2 (The Associative Law for Multiplication): For any three numbers a, b, and c, a(bc) = (ab)c
M3 (Multiplicative Identity): For any number a, 1a = a
D (Distributive Law): For any three numbers a, b, and c, (a + b)c = ac + bc
Using these rules explicitly, prove that 0 × 0 = 0
-
1) Prove there are infinitely many primes.
Assume for contradiction that there are finitely many primes. Let the primes be 2, 3, 5, …, P for some largest prime P.
Consider the number N = 2 × 3 × 5 x … x P + 1. Either N is a prime or a composite number.
If N is prime, then N must be in the list of primes 2, 3, 5,…,P but N is clearly bigger than P. This is a contradiction.
If N is a composite number, then N must be divisible by a prime in the list 2, 3, 5, …, P. On inspection, each prime leaves a remainder of 1 when dividing into N. This is a contradiction.
Hence, by contradiction, there are infinitely many prime numbers.
2) Prove that the square root of 2 is irrational.
Assume for contradiction that the square root of 2 is rational. Then, it can be expressed as sqrt(2) = A/B where A and B have no common factors. The fraction is simplified as far as possible.
Squaring both sides gives 2 = A²/B² and multiplying both sides by B² gives A² = 2B².
A² is even so A is even (proof of this left to reader). We can write A as A = 2k for some integer k. Then, A² = 4k².
Substituting into equation with B gives 4k² = A² = 2B² so B² = 2k². B² is even and so B is also even. Hence, A and B are both even so have a common factor of 2. This is a contradiction.
Hence, the square root of 2 is irrational.
3) Below are some laws of addition and multiplication.
A1 (The Commutative Law for Addition): For any two numbers a and b, a + b = b + a
A2 (The Associative Law for Addition): For any three numbers a, b, and c, a + (b + c) = (a + b) + c
A3 (Additive Identity): For any number a, 0 + a = a
M1 (The Commutative Law for Multiplication): For any two numbers a and b, ab = ba
M2 (The Associative Law for Multiplication): For any three numbers a, b, and c, a(bc) = (ab)c
M3 (Multiplicative Identity): For any number a, 1a = a
D (Distributive Law): For any three numbers a, b, and c, (a + b)c = ac + bc
Using these rules explicitly, prove that 0 x 2 = 0, where 2 is defined as 2 = 1 +1
0 × 2 = 0 x (1 + 1) by definition
= (1 + 1) x 0 by M1
= 1 × 0 + 1 × 0 by D
= 0 + 1 × 0 by M3
= 0 + 0 by M3
= 0 by A3
4) Below are some laws of addition and multiplication.
A1 (The Commutative Law for Addition): For any two numbers a and b, a + b = b + a
A2 (The Associative Law for Addition): For any three numbers a, b, and c, a + (b + c) = (a + b) + c
A3 (Additive Identity): For any number a, 0 + a = a
M1 (The Commutative Law for Multiplication): For any two numbers a and b, ab = ba
M2 (The Associative Law for Multiplication): For any three numbers a, b, and c, a(bc) = (ab)c
M3 (Multiplicative Identity): For any number a, 1a = a
D (Distributive Law): For any three numbers a, b, and c, (a + b)c = ac + bc
Using these rules explicitly, prove that 0 × 0 = 0
0 x 0 = 0 + 0 x 0 by A3
= 0 x 0 + 0 by A1
= 0 x 0 + 1 x 0 by M3
= ( 0 + 1 ) x 0 by D
= 1 x 0 by A3
= 0 by M3
Personalized Tutoring
Personalized sessions for students from middle school to college and university. Prices start from $50. By the end of the session, students will confidently say “It’s that easy”.
Public Lectures
Engaging talks on a variety of mathematical topics open to everyone. Has a certain mathematics topic always had your interest? Come learn about it in a public lecture.
Mathematics Olympiad
Problem-solving challenges to spark mathematical creativity and foster intellectual competition. How do you compare against the other great minds on the island?
Personalized Tutoring
Upcoming Public Lecture
There are no public lectures currently scheduled. Please check back soon!
-
Patterns, Primes, and Proofs: The Building Blocks of Mathematics
A Piece of Cake: Everything about Fractions
Winter Mathematics Olympiad 2026
Do you have what it takes?
Date and Time
28 Feb 2026 at 3 pm (1 hour)
Entrance Fee
$20
Spaces are limited. Please register for venue details.
The Bermuda Mathematics Academy is proud to host its first Mathematics Olympiad.
This premier competition invites the island’s best and brightest problem solvers to tackle challenging mathematical problems that reward creativity, logical reasoning, and thinking outside the box.
The Olympiad is open to everyone aged 14 and over, including both students and adults. If you ever wondered how your mathematical skills compare against others, this is your opportunity to find out.
Participants will have exactly one hour to solve 10 carefully selected Olympiad problems designed to push your thinking and stretch your intuition.
Top-performing students will be considered for selection to the Bermuda team attending international mathematics competitions, including the International Mathematics Olympiad.
Spaces are limited. Check-in opens at 2:45 pm with a prompt start at 3:00 pm. Participants only need something to write with. No calculators required. Full answers and award ceremony to follow at later date. Schools may sponsor students if desired.
Contact us
hello@maths.bm